What is it? – KRACH is short for “Ken’s Rating for American College Hockey.” Ken is Ken Butler, a statistician, and the mathematical model he used is known as the Bradley-Terry Rating System.
- The KRACH rating system is an attempt to combine the performance of each team with the strength of the opposition against which that performance was achieved, and to summarize the result as one number, a “rating”, for each team. The higher the rating, the better the team.
- KRACH accounts for strength-of-schedule (SOS) as it ranks the teams.
- KRACH is calculated purely from the results(win/loss/tie) and does not use goals scored or goal differential like myhockeyrankings.
- Overtime wins count as wins.
Why we use it rather than points? – KRACH ratings are used instead of traditional points for the following reason:
- Teams play an unbalanced schedule, teams will not play all the teams in teams’ age division
- Teams that play a more difficult schedule would be unfairly punished in the traditional points-based standings
- KRACH does not put greater emphasis on blowing out teams like myhockeyrankings
- The THF offers 2 season structures, full-season and partial season. Using KRACH rather than points earned will allow for fair rankings such that teams playing fewer games are fairly measured within their division
What is the process for the Federations – The KRACH algorithm is written in python and consists of a data organization routine and an iterative strength of schedule solver.
- The algorithm takes the Team win loss data from an excel file output by the GameSheet online scoring platform used to store game data.
- This data is then organized by division using tags provided by GameSheet.
- This divisional data is then organized into pairwise comparisons based on wins and losses to feed into the solver.
- The pairwise team input can be visualized as a matrix with each time represented as a row and wins against other teams in the columns.
| Team A | Team B | Team C | Team D | |
| Team A | – | 2 | 0 | 1 |
| Team B | 3 | – | 5 | 0 |
| Team C | 0 | 3 | – | 1 |
| Team D | 4 | 0 | 3 | – |
The solver utilizes a Bradley-Terry model to solve for rankings (P) using the paired comparisons. Pairwise means that given a pair of teams i and j drawn from a population P the algorithm estimates the probability that team i will win over team j:
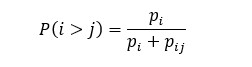
To get to this probability an iterative algorithm with “regularization scheme” and pairwise team win records are used. Per the CHN a logistic regression is used as the solver of the iterative algorithm. The regularization scheme used is an ‘alpha value,’ a regularization scheme so that the solver does not go to infinity when teams have zero wins. The alpha value is 0.85 for every team input as a win against a ‘Dummy Team’. This is because you cannot have zero as the numerator.
The solver then initiates a ranking of 1 for every team, then solves the following equation for each team. The ellipses (…) at the end of the equation represents the sub formula for Team A (Tm A) against Teams C and D.
P Tm A = Total Wins Tm A / ( Sum ( (Losses Tm A vs. Tm B) / (P Tm A + P Tm B), …)
The new P values for each team are calculated using the existing P values as shown above for Team A. These values replace the 1s used to initiate the algorithm. The same calculations are conducted on the new P values for the next iteration of the algorithm. This is repeated 200 times or until the difference of P values between iterations is less than 0.00001. The output (P) is then scaled by 10,000 to make the results all over 1. The iterative nature of the algorithm allows for the strength of schedule to be taken into account automatically without any initial rankings. Thus, no initial rankings are made by hand and no favoritism is possible. Strength of schedule is included in the calculated P value by including the P values of all teams played while calculating each team.
Sources:
https://en.wikipedia.org/wiki/Bradley%E2%80%93Terry_model
https://www.collegehockeynews.com/info/?d=krach
https://github.com/bjlkeng/Bradley-Terry-Model/blob/master/update_model.py


